ベルヌーイの定理とは
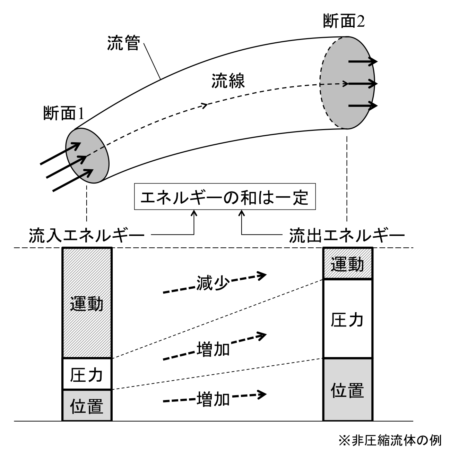
ベルヌーイの定理(Bernoulli’s theorem)とは、流体内のエネルギーの和が流線上で常に一定であるという定理です。
流体のエネルギーには運動・位置・圧力・内部エネルギーの4つあり、非圧縮性流体であれば内部エネルギーは無視できます。
位置エネルギーの変化を無視できる流れを考えると、運動エネルギーと圧力のエネルギーの和が一定になります。
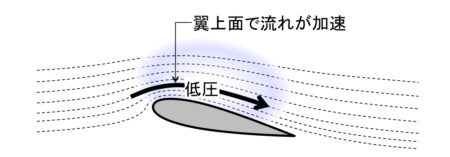
すなわち「流れの圧力が上がれば速度は低下し、圧力が下がれば速度は上昇する」という流れの基本的な性質をベルヌーイの定理は表しています。
ベルヌーイの定理には、圧縮性流体と非圧縮性流体の2つの公式があります。
圧縮性流体のベルヌーイの定理
\( \displaystyle \underset{\text{運動}} { \underline{ \frac{v^2}{2} }} + \underset{\text{位置}} { \underline{ g h }} + \underset{\text{圧力+内部}} { \underline{ \frac{\gamma}{\gamma-1} \frac{p}{\rho} }} = const. \tag{1} \)
非圧縮性流体のベルヌーイの定理
\( \displaystyle \underset{\text{運動}} { \underline{ \frac{v^2}{2} }} + \underset{\text{位置}} { \underline{ g h }} + \underset{\text{圧力}} { \underline{ \frac{p}{\rho} }} = const. \tag{2} \)
| \(\rho\) | 流体の密度 [kg/m3] |
| \(v\) | 流体の速度 [m/s] |
| \(g\) | 重力加速度 [m/s2] |
| \(h\) | 流体の高さ [m] |
| \(p\) | 流体の圧力 [kg/m2] |
| \(\gamma\) | 比熱比 |
(参考:航空力学の基礎(第2版), P.33 (2.46),(2.52)式)
圧縮性流体のベルヌーイの定理の導出
断面1と2を通過する圧縮性流体のエネルギーを計算します。流れは時間変化のない定常流、流体は摩擦のない非粘性流体とします。
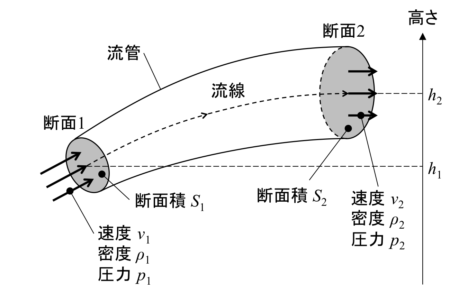
断面1と2を通過する流体の各エネルギーは、流体の質量を \(m\) [kg]とすると以下の通りです。
| 断面1(流入) | 断面2(流出) | |
| 運動エネルギー | \(\displaystyle \frac{1}{2} m {v_1}^2\) | \(\displaystyle \frac{1}{2} m {v_2}^2\) |
| 位置エネルギー | \(m g h_1\) | \(m g h_2\) |
| 内部エネルギー | \( \displaystyle \frac {m}{\gamma – 1} \frac {p_1}{\rho_1} \) | \( \displaystyle \frac {m}{\gamma – 1} \frac {p_2}{\rho_2} \) |
| 圧力エネルギー | \(\displaystyle m \frac {p_1}{\rho_1} \) | \( \displaystyle m \frac {p_2}{\rho_2} \) |
断面1と2を通過する流体はエネルギーの時間変化はなく流管の外部に仕事をしません。したがって、流体のエネルギーの和は断面1と2で等しいから
\(\displaystyle \underset{\text{運動}} { \underline{ \frac{1}{2} m {v_1}^2 }} + \underset{\text{位置}} { \underline{ m g h_1}}+ \underset{\text{内部}} { \underline{ \frac {m}{\gamma – 1} \frac {p_1}{\rho_1} }} + \underset{\text{圧力}} { \underline{ m \frac {p_1}{\rho_1}}} = \underset{\text{運動}} { \underline{ \frac{1}{2} m {v_2}^2}} + \underset{\text{位置}} { \underline{ m g h_2}} + \underset{\text{内部}} { \underline{ \frac {m}{\gamma – 1} \frac {p_2}{\rho_2}}} + \underset{\text{圧力}} { \underline{ m \frac {p_2}{\rho_2}}} = const. \tag{3} \)
上式を流体の質量 \(m\) で割り内部エネルギーと圧力エネルギーの項をまとめると、圧縮性流体のベルヌーイの定理が得られます。
\(\displaystyle \underset{\text{運動}} { \underline{ \frac{1}{2} {v_1}^2}} + \underset{\text{位置}} { \underline{ g h_1}}+\underset{\text{内部+圧力}} { \underline{ \frac {\gamma}{\gamma – 1} \frac {p_1}{\rho_1}}} = \underset{\text{運動}} { \underline{ \frac{1}{2} {v_2}^2}} + \underset{\text{位置}} { \underline{ g h_2}} + \underset{\text{内部+圧力}} { \underline{ \frac {\gamma}{\gamma – 1} \frac {p_2}{\rho_2}}} = const. \tag{4} \)
(参考:航空力学の基礎(第2版), P.33 (2.51)式)
このようにベルヌーイの定理は流体におけるエネルギー保存の法則といえます。
内部エネルギーと圧力エネルギーはエンタルピーの式から計算します。
\(\displaystyle H=mh=m \left ( e+ \frac {p}{\rho} \right ) \tag{5} \)
| \(H\) | エンタルピー [J] |
| \(m\) | 流体の質量 [kg] |
| \(h\) | 比エンタルピー(単位質量あたりのエンタルピー) [J/kg] |
| \(e\) | 比内部エネルギー(単位質量あたりの内部エネルギー) [J/kg] |
| \(p\) | 流体の圧力 [Pa] |
| \(\rho\) | 流体の密度 [kg/m3] |
(参考:航空力学の基礎(第2版), P.21 (2.11)式)
内部エネルギーは、流体を完全気体として完全気体の内部エネルギーの式・完全気体の状態方程式・マイヤーの関係式・比熱比の関係式から計算します。
- 完全気体の比内部エネルギーの関係式(単位質量あたり)
\( e=C_v T \tag{6}\)
| \(e\) | 完全気体の比内部エネルギー [J/kg](単位質量あたりの内部エネルギー) |
| \(C_v\) | 定積モル比熱 [J/(kg・K)] |
| \(T\) | 完全気体の温度 [K] |
(参考:航空力学の基礎(第2版), P.22 (2.14)式)
- 完全気体の状態方程式
\( \displaystyle \frac{p}{\rho}=RT \tag{7}\)
| \(p\) | 完全気体の圧力 [Pa] |
| \(\rho\) | 完全気体の密度 [kg/m3] |
| \(T\) | 完全気体の温度 [K] |
| \(R\) | 気体定数 [J/(kg・K)] |
(参考:航空力学の基礎(第2版), P.18 (2.3a)式を変形)
- マイヤーの関係式
\( C_p – C_v = R \tag{8}\)
| \(C_p\) | 定圧モル比熱 [J/(kg・K)] |
| \(C_v\) | 定積モル比熱 [J/(kg・K)] |
| \(R\) | 気体定数 [J/(kg・K)] |
(参考:航空力学の基礎(第2版), P.21 (2.12)式)
- 比熱比の関係式
\( \displaystyle \gamma = \frac{C_p}{C_v} \tag{9}\)
| \(\gamma\) | 比熱比 [−] |
| \(C_p\) | 定圧モル比熱 [J/(kg・K)] |
| \(C_v\) | 定積モル比熱 [J/(kg・K)] |
(参考:航空力学の基礎(第2版), P.21 (2.13)式)
- 最終的な比内部エネルギーの計算式
(6)式を(7)〜(9)式を用いて変形すると最終的な比内部エネルギーの計算式は
\( \displaystyle e=\frac {1}{\gamma – 1} \frac {p}{\rho} \tag{10} \)
(参考:航空力学の基礎(第2版), P.22 (2.14)式)
非圧縮性流体のベルヌーイの定理の導出
非圧縮性流体の場合、流体は圧縮されないので流体の内部エネルギーは変化しません。従って(3)式の内部エネルギーの項を省略できます。
\(\displaystyle \underset{\text{運動}} { \underline{ \frac{1}{2} m {v_1}^2 }} + \underset{\text{位置}} { \underline{ m g h_1}} + \underset{\text{圧力}} { \underline{ m \frac {p_1}{\rho_1}}} = \underset{\text{運動}} { \underline{ \frac{1}{2} m {v_2}^2}} + \underset{\text{位置}} { \underline{ m g h_2}} + \underset{\text{圧力}} { \underline{ m \frac {p_2}{\rho_2}}} = const. \tag{11} \)
上式を流体の質量 \(m\) で割ると非圧縮性流体のベルヌーイの定理が得られます。
\(\displaystyle \underset{\text{運動}} { \underline{ \frac{1}{2} {v_1}^2}} + \underset{\text{位置}} { \underline{ g h_1}}+\underset{\text{圧力}} { \underline{ \frac {p_1}{\rho_1}}} = \underset{\text{運動}} { \underline{ \frac{1}{2} {v_2}^2}} + \underset{\text{位置}} { \underline{ g h_2}} + \underset{\text{圧力}} { \underline{ \frac {p_2}{\rho_2}}} = const. \tag{12} \)
(参考:航空力学の基礎(第2版), P.22 (2.44)式)
まとめ
- ベルヌーイの定理とは、流体におけるエネルギー保存則。
- 圧縮性流体では、流線上で運動・位置・内部・圧力エネルギーの和が一定。
- 非圧縮性流体では、流線上で運動・位置・圧力エネルギーの和が一定。
参考資料
- 航空力学の基礎(第2版)
次の記事
次の記事では、ベルヌーイの定理から得られる流体の静圧と動圧について解説します。




コメントを残す