圧力係数とは
圧力係数(Pressure coefficient)とは流体の静圧を無次元で表した係数で、一様流の静圧からの変化分を一様流の動圧で割ることで得られます。
\( \displaystyle C_p= \frac{p \ – p_\infty}{ \displaystyle \frac{1}{2}\rho_\infty {V_\infty}^2} \tag{1}\)
| \(C_p\) | 圧力係数 [−] |
| \(p\) | 流体の静圧 [Pa] |
| \(p_\infty\) | 一様流の静圧 [Pa] |
| \(\rho_\infty\) | 一様流の密度 [kg/m3] |
| \(V_\infty\) | 一様流の速度 [m/s] |
(参考:航空力学の基礎(第2版), P.44 (2.68)式)
圧力を無次元で表す理由

レイノルズ数とマッハ数が一致する流れでは物体の大きさに関係なく、物体形状が相似であれば圧力係数も同じになります。(流れの相似則といいます。)
圧力を無次元で表すことにより、物体形状の影響を見ることができます。
正圧と負圧
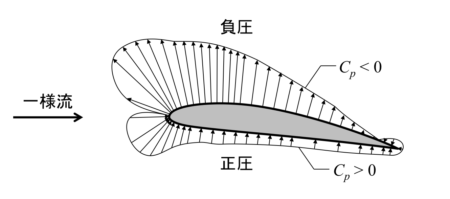
圧力係数は一様流の圧力に対して高いか低いかを表しています。一様流の圧力より高ければ正圧(Positive pressure)、低ければ負圧(Negative pressure)といいます。
正圧であれば物体は流体に押され、負圧であれば物体は流体に吸われて引っ張られるような作用を受けていることになります。
圧力係数の値が表す意味

圧力係数は、一様流静圧からの変化分(\( p \ – p_\infty \))を一様流動圧(\( \displaystyle \frac{1}{2}\rho_\infty {V_\infty}^2\))で割った値です。すなわち、流体の静圧が一様流動圧の何倍増減したかを示しています。
例えば流体の圧力係数が2の場合、流体の静圧は一様流動圧の2倍増加したことを意味します。
まとめ:圧力係数
- 圧力係数とは、流体の圧力を無次元で表した係数のこと。
- 圧力係数の値は、流体の静圧が一様流動圧の何倍増減したかを表す。
参考資料
- 航空力学の基礎(第2版)


コメントを残す