この記事では、空力中心と風圧中心の違いについて解説します。また実際の翼型の風洞試験データから空力中心を計算する方法についても計算例とともに解説します。
空力中心と風圧中心の違い
空力中心とは
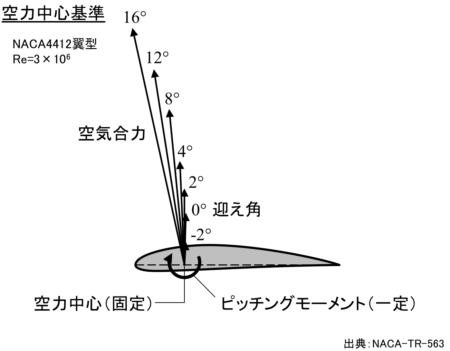
空力中心(aerodynamic center)とは、空気力を空力中心に定義したとき迎え角により空力中心まわりのピッチングモーメントが変化しない点のことです。翼型のコード長25%付近にあります。
空力性能の迎え角による変化を見る際、空気力の変化だけに注目すれば良いので、扱いやすいメリットがあります。
風圧中心とは
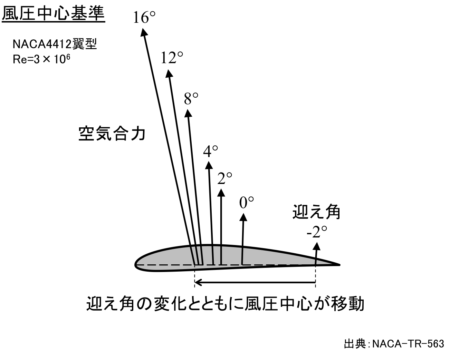
風圧中心(center of pressure)とは、空気力が実際に作用している点のことです。
直感的で分かりやすいものの、迎え角が変化すると風圧中心(空気力の定義点)も移動するため、扱いずらいデメリットがあります。
空力中心の計算方法
25%コード長基準のデータから空力中心を計算する方法を解説します。(風洞試験データは通常25%コード長基準で整理されています。)
サンプル計算に使用する空力特性データ
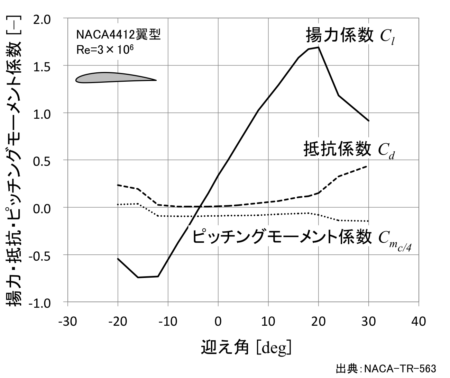
サンプル計算ケースとして、NACA-TR-563に記載されているNACA4412翼型の空力特性データ(25%コード長基準のデータ)を使用します。
準備するデータは25%コード長基準での揚力係数・抵抗係数・ピッチングモーメント係数の各迎え角データです。
空力中心の算出手順
- 法線分力係数 \( C_n \) の計算
- 前縁まわりのピッチングモーメント係数 \( C_{m_0} \) の計算
- 縦軸 \( C_{m_0} \) ・横軸 \( C_n \) のグラフから近似直線を作成
近似直線の傾きが空力中心の位置を表し、切片が空力中心まわりのピッチングモーメント係数となります。
①法線分力係数の計算
前縁まわりのピッチングモーメント係数を計算するために、空気力をコード線に垂直な成分(法線分力)に分解します。
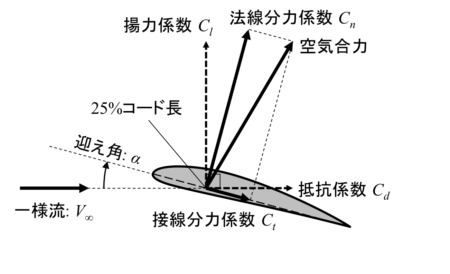
\( C_n = C_l \cos \left ( \alpha \right ) + C_d \sin \left (\alpha \right ) \tag{1}\)
| \(C_n\) | 法線分力係数 [−] |
| \(C_l\) | 揚力係数 [−] |
| \(C_d\) | 抵抗係数 [−] |
| \(\alpha\) | 迎え角 [deg] |
計算結果
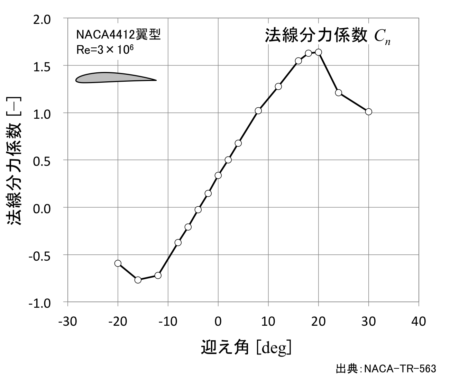
②前縁まわりのピッチングモーメント係数の計算
前縁まわりのピッチングモーメント係数を計算します。
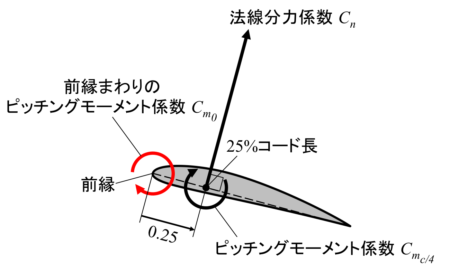
風洞試験データは25%コード長基準のデータなので、計算式は以下の通りです。
\(\displaystyle C_{m_0}= -0.25 \times C_n + C_{m_{c/4}} \tag{2} \)
計算結果
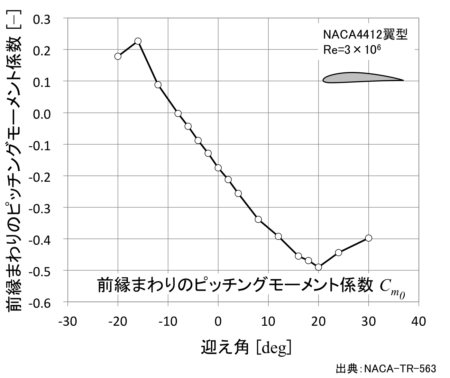
③近似直線の作成
前縁まわりのピッチングモーメントは法線分力により変化するので、縦軸 \( C_{m_0} \) ・横軸 \( C_n \) のグラフを見てみましょう。
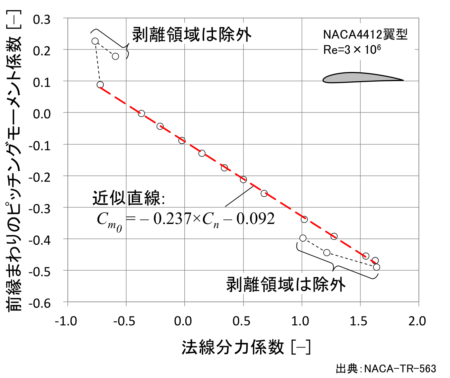
剥離領域を除外して近似直線\( \left ( y=ax+b \right ) \)を作成すると以下のようになります。
\( C_{m_0} = \underset{\text{空気力に依存する項}}{ \underline{-0.237 \times C_n } } \, \underset{\text{定数}} { \underline{- 0.092} } \tag{3}\)
前縁まわりのピッチングモーメントは、空気力に依存する項(第1項)と空気力に依存しない定数(第2項)で表すことができます。
この式の意味を考えるために再度定義図を確認します。
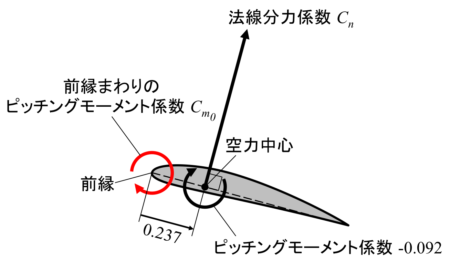
\( C_{m_0} = – \underset{\text{空力中心}}{ \underline{0.237 } } \times C_n \, \underset{C_{m_{a.c.}}} { \underline{- 0.092} } \tag{4}\)
上の式の「0.237」が前縁からの距離、すなわち空力中心位置に相当します。「-0.092」が追加するピッチングモーメント\(C_{m_{a.c.}}\)です。
すなわち、23.7%コード長位置に空気力を定義し、「-0.092」のピッチングモーメントを追加すれば、風圧中心基準の空気力と等価になります。
この場合、翼の迎え角が変わっても空気力の作用点は移動せずピッチングモーメントも一定です。
このような点を空力中心といいます。
理論的には空力中心は25%コード長にあり、実際の様々な翼型でも25%付近にあることが確認されています。(今回の計算では23.7%コード長でした。)
まとめ


- 空力中心とは、迎え角により空力中心まわりのピッチングモーメントが変化しない点のこと。
- 風圧中心とは、空気力が実際に作用している点のこと。迎え角が変わると移動するため扱いづらい。
参考資料
次の記事
次の記事では、翼型の基本的な空力特性の見方について解説します。




コメントを残す