連続の式とは
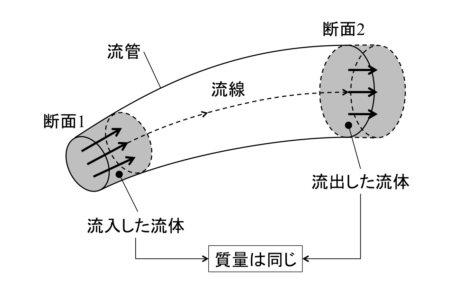
連続の式(continuity equation)とは、流体の質量流量は流線上のどの断面でも常に一定であるという定理です。
単位時間あたりに断面を通過する流体の質量のこと。単位は[kg/s]
圧縮性流体の連続の式
\(\rho v S=const. \tag{1}\)
非圧縮性流体の連続の式
\(v S=const. \tag{2}\)
| \(\rho\) | 流体の密度 [kg/m3] |
| \(v\) | 流体の速度 [m/s] |
| \(S\) | 断面積 [m2] |
(参考:航空力学の基礎(第2版), P.30 (2.38a),(2.38b)式)
圧縮性流体の連続の式の導出
時間的変化のない定常流として、断面1と2を通過する流体の質量流量を計算します。
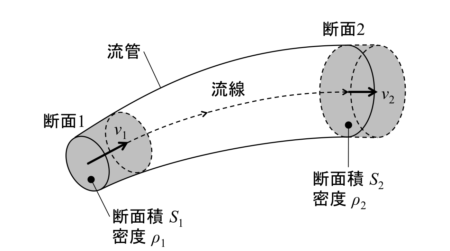
断面1の流体の速度を\(v_1\)とすると、単位時間に通過する流体の体積(流量)は
\(v_1 S_1 \tag{3}\)
流体の密度を\(\rho_1\)とすると、単位時間に通過する流体の質量流量は
\(\rho_1 v_1 S_1 \tag{4}\)
断面2についても同様に、断面2を単位時間に通過する流体の質量流量は
\(\rho_2 v_2 S_2 \tag{5}\)
定常流なので断面1と断面2の間の流管の質量は時間的に変化しません。そのため断面1に流入する質量流量と断面2から流出する質量流量は等しくなるので
\( \underset{\text{断面1}}{\underline {\rho_1 v_1 S_1}}=\underset{\text{断面2}}{\underline {\rho_2 v_2 S_2}}=const. \tag{6}\)
このように連続の式は流体における質量保存の法則といえます。
非圧縮性流体の連続の式の導出
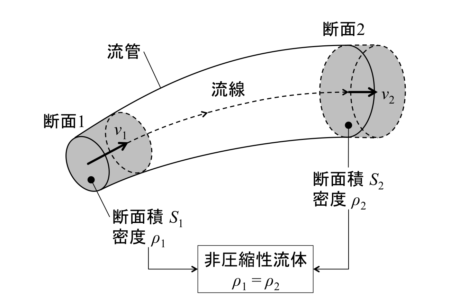
非圧縮性流体では流体の密度は変化しないので
\(\rho_1=\rho_2 \tag{7}\)
よって、(6)の連続の式は以下のように体積流量の形に簡略化されます。
\( \underset{\text{断面1}}{\underline {v_1 S_1}}=\underset{\text{断面2}}{\underline {v_2 S_2}}= const. \tag{8}\)
非圧縮性流体の連続の式は、水やマッハ数0.3以下の空気などに使用します。
単位時間あたりに断面を通過する流体の体積のこと。単位は[m3/s]。
まとめ
- 連続の式とは、流体の質量流量は流線上のどの断面でも常に一定であるという定理である。
- 圧縮性流体では流線上で質量流量が一定である。
- 非圧縮性流体では流線上で体積流量が一定である。
参考資料
- 航空力学の基礎(第2版)
次の記事
次の記事では、流れにおいてもう一つ重要な法則である「ベルヌーイの定理」について解説します。




コメントを残す