この記事では、標準大気の例としてU.S. standard atmosphere, 1976に基づいて、各高度における空気の温度・圧力・密度・音速・粘性係数・動粘性係数の計算式を解説します。
高度を入力すれば誰でもすぐに大気の状態を計算できるように定式化しました。(理科年表を見れば良いのですが有料で公開されていません。)
標準大気とは
標準大気とは、地球の大気の圧力・温度・密度・粘度などが高度によってどのように変化するのかを表した標準となる大気のモデルです。
ここではU.S. standard atmosphere, 1976に基づいて、空気の状態の計算式を紹介します。
高度0kmでの空気の温度・圧力・密度・音速・粘性係数・動粘性係数
高度0kmの空気の物性値はよく使用するので一覧で値を掲載します。
| 項目 | 値(高度0km) |
| 空気の温度 \(T_0\) | 15 [℃] |
| 空気の圧力 \(P_0\) | 101325 [Pa] |
| 空気の密度 \(\rho_0\) | 1.225 [kg/m3] |
| 空気の音速 \(a_0\) | 340.29 [m/s] |
| 空気の粘性係数 \(\mu_0\) | 1.7894×10-5 [Ns/m2] |
| 空気の動粘性係数 \(\nu_0\) | 1.4607×10-5 [m2/s] |
(出典:U.S. standard atmosphere, 1976, P.52 Table I, P.100 Table III)
高度0~86kmでの空気の温度・圧力・密度・音速・粘性係数・動粘性係数
高度とジオポテンシャル高度の関係式
U.S. standard atmosphere, 1976での空気の物性(温度・圧力等)の計算式では、通常の物差しで計るような長さの「高度」ではなく「ジオポテンシャル高度」という位置エネルギーを基準とした高度を使用します。
高度 \(Z\) とジオポテンシャル高度 \(H\) の関係式は以下の通りです。
\(\displaystyle H= \frac{r_0 Z}{r_0+Z} \tag{1}\)
\(\displaystyle Z= \frac{r_0 H}{r_0-H} \tag{2}\)
| \(H\) | ジオポテンシャル高度 [km’] |
| \(Z\) | 高度 [km] |
| \(r_0\) | 北緯45度での地球の半径: 6356.766[km] |
(出典:U.S. standard atmosphere, 1976, P.2 Table 2, P.8 (18),(19)式)
空気の温度の計算式
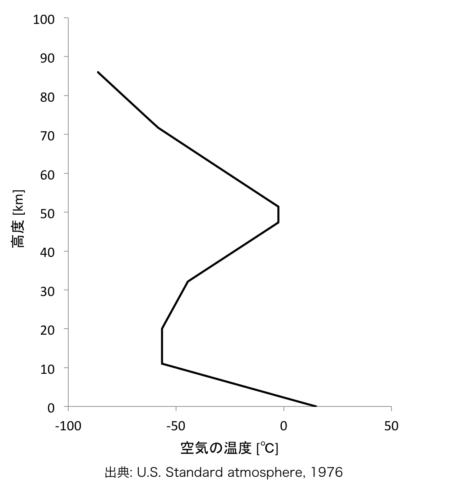
空気の温度は高度によって温度勾配が異なるため、高度による場合分けを行います。
| ジオポテンシャル高度 \(H\) [km’] | 空気の温度 \(T\) [℃]の計算式 . |
| \(0 \le H \le 11\) | \(T=15-6.5H\) |
| \(11 \le H \le 20\) | \(T=-56.5\) |
| \(20 \le H \le 32\) | \(T=-76.5+H\) |
| \(32 \le H \le 47\) | \(T=-134.1+2.8H\) |
| \(47 \le H \le 51\) | \(T=-2.5\) |
| \(51 \le H \le 71\) | \(T=140.3-2.8H\) |
| \(71 \le H \le 84.852\) | \(T=83.5-2H\) |
(出典:U.S. standard atmosphere, 1976, P.3 Table 4, P.10 (23)式より算出)
空気の圧力の計算式
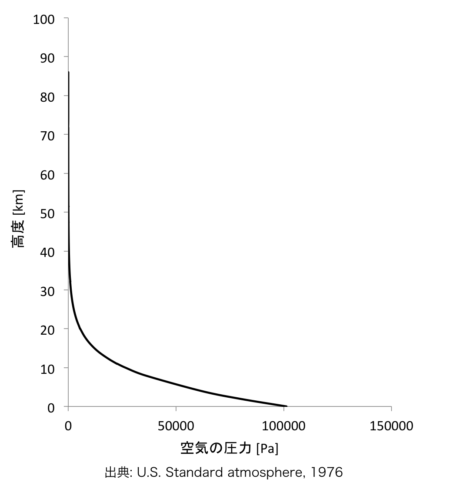
空気の圧力は空気の温度勾配の有無で計算式が変わるので、空気の温度の計算式と同様に高度による場合分けを行います。
| ジオポテンシャル高度 \(H\) [km’] | 空気の圧力 \(P\) [Pa]の計算式 . |
| \(0 \le H \le 11\) | \(\displaystyle P=101325 \times \left( \frac{288.15}{T+273.15} \right) ^{-5.256}\) |
| \(11 \le H \le 20\) | \(P=22632.064 \times e^{-0.1577(H-11)}\) |
| \(20 \le H \le 32\) | \(\displaystyle P=5474.889 \times \left( \frac{216.65}{T+273.15} \right) ^{34.163}\) |
| \(32 \le H \le 47\) | \(\displaystyle P=868.019 \times \left( \frac{228.65}{T+273.15} \right) ^{12.201}\) |
| \(47 \le H \le 51\) | \(P=110.906 \times e^{-0.1262(H-47)}\) |
| \(51 \le H \le 71\) | \(\displaystyle P=66.939 \times \left( \frac{270.65}{T+273.15} \right) ^{-12.201}\) |
| \(71 \le H \le 84.852\) | \(\displaystyle P=3.956 \times \left( \frac{214.65}{T+273.15} \right) ^{-17.082}\) |
(出典:U.S. standard atmosphere, 1976, P.12 (33a), (33b)式より算出)
空気の密度の計算式
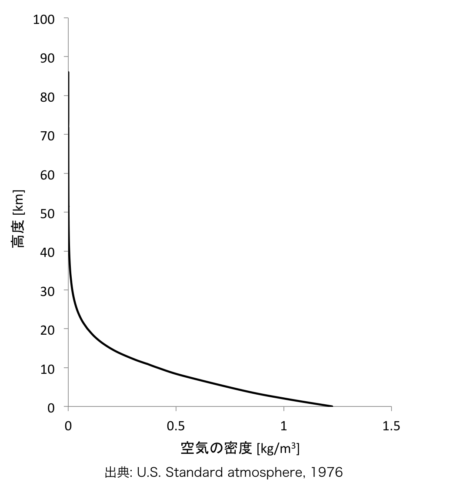
空気の密度は、空気の温度と圧力から計算できます。
\(\displaystyle \rho= \frac{P \cdot M_0}{R^* \cdot T_M}= \frac{0.0034837P}{T+273.15} \tag{3}\)
| \(\rho\) | 空気の密度 [kg/m3] |
| \(P\) | 空気の圧力 [Pa] |
| \(M_0\) | 高度0kmでの大気の平均分子量: 28.9644 [kg/kmol] |
| \(R^*\) | 気体定数: 8.31432×103 [Nm/(kmol・K)] |
| \(T_M\) | 空気の温度 [K] (\(T_M=T+273.15\)) |
| \(T\) | 空気の温度 [℃] |
(出典:U.S. standard atmosphere, 1976, P.15 (42)式)
空気の音速の計算式
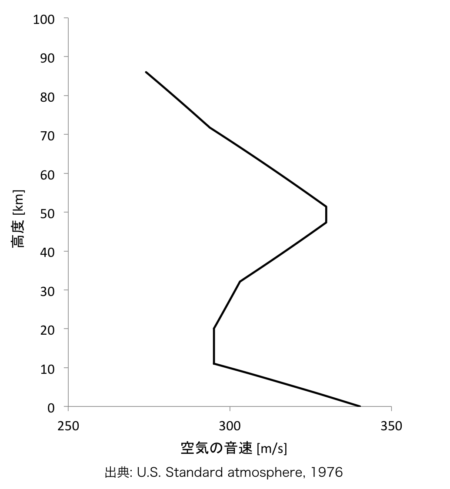
空気の音速は、空気の温度から計算できます。
\(\displaystyle a= \sqrt {\frac {\gamma \cdot R^* \cdot T_M}{M_0}} = 20.0468\sqrt { \left( T+273.15 \right) } \tag{4} \)
| \(a\) | 空気の音速 [m/s] |
| \(\gamma\) | 空気の比熱比: 1.4 [−] |
| \(M_0\) | 高度0kmでの大気の平均分子量: 28.9644 [kg/kmol] |
| \(R^*\) | 気体定数: 8.31432×103 [Nm/(kmol・K)] |
| \(T_M\) | 空気の温度 [K] (\(T_M=T+273.15\)) |
| \(T\) | 空気の温度 [℃] |
(出典:U.S. standard atmosphere, 1976, P.18 (50)式)
空気の粘性係数の計算式
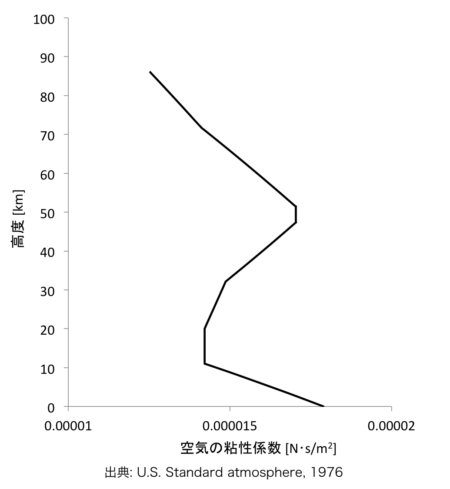
空気の粘性係数は、空気の温度から計算できます。
\( \displaystyle \mu = \frac {\beta \cdot {T_M}^{\frac{3}{2}}}{T_M+S} = 1.458 \times 10^{-6} \times \frac { \left( T + 273.15 \right) ^{\frac{3}{2}}}{T+383.55} \tag{5}\)
| \(\mu\) | 空気の粘性係数 [N・s/m2] |
| \(\beta\) | 定数: 1.458×10-6 [kg/(s・m・K1/2)] |
| \(S\) | サザーランドの定数: 110.4 [K] |
| \(T_M\) | 空気の温度 [K] (\(T_M=T+273.15\)) |
| \(T\) | 空気の温度 [℃] |
(出典:U.S. standard atmosphere, 1976, P.19 (51)式)
空気の動粘性係数の計算式
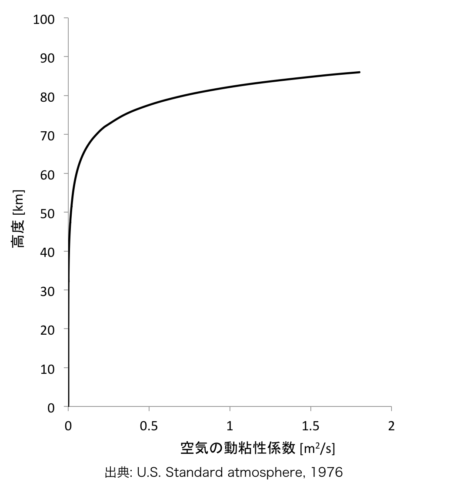
空気の動粘性係数は、空気の粘性係数と密度から計算できます。
\(\displaystyle \nu= \frac {\mu}{\rho} \tag{6}\)
| \(\nu\) | 空気の動粘性係数 [m2/s] |
| \(\mu\) | 空気の粘性係数 [N・s/m2] |
| \(\rho\) | 空気の密度 [kg/m3] |
(出典:U.S. standard atmosphere, 1976, P.19 (52)式)
まとめ:標準大気
- 大気の状態は高度を入力として式で計算できる。
- 高度には、通常の高度とジオポテンシャル高度があるので注意すること。
参考資料
次の記事
大気の講座はこれで終了です。次の講座では、流体の流れについて解説します。




初心者に分かり安く解説有難うございます。