この記事では、亜音速の翼型の空気抵抗についてFluid-Dynamic Dragに掲載されている簡易的な推算方法を紹介します。
翼型の空気抵抗の計算方法
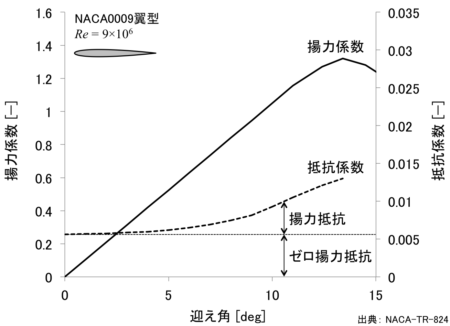
翼型に生じる空気抵抗 \( C_d \) を、揚力が発生していない時の空気抵抗(ゼロ揚力抵抗) \( C_{d_0} \) と揚力が発生することによって生じる抵抗(揚力抵抗) \( C_{d_l} \) の2つに分解します。
\( C_d = C_{d_0} + C_{d_l} \tag{1}\)
| \(C_d\) | 翼型の抵抗係数 [−] |
| \(C_{d_0}\) | ゼロ揚力抵抗係数 [−] |
| \(C_{d_l}\) | 揚力抵抗係数 [−] |
翼型に揚力が発生すると翼上面の流れはゼロ揚力の時より加速し境界層が発達します。境界層の発達によって生じる粘性による抵抗(摩擦抵抗と圧力抵抗)を揚力抵抗と呼んでいます。
翼型のゼロ揚力抵抗の推算
翼型のゼロ揚力抵抗は平板の摩擦抵抗をベースに計算します。
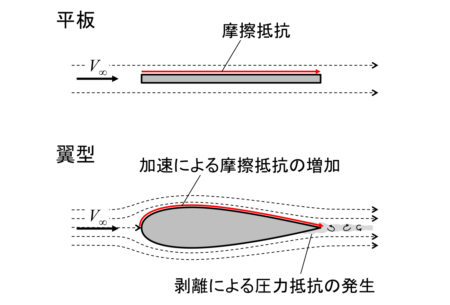
計算の際には平板との違いとして以下の2点を考慮します。
- 翼の膨らみ(翼厚)部分の流れの加速による摩擦抵抗の増加
- 翼型の後方で生じる剥離による圧力抵抗の発生
以上のことから翼型の空気抵抗は翼厚によって変化すると考え、翼厚比の関数としてゼロ揚力抵抗を計算します。
層流領域(Re = 1 ~ 5×104)
\( \displaystyle C_{d_0} = \underset{\text{摩擦抵抗}} { \underline{ 2C_f \left ( 1 + \frac{t}{c} \right ) }} + \underset{\text{圧力抵抗}} { \underline{ \left ( \frac{t}{c} \right )^2 }} \tag{2} \)
| \(C_{d_0}\) | ゼロ揚力抵抗係数 [−] |
| \(C_f\) | 平板の摩擦抵抗係数 [−] |
| \( \displaystyle \frac{t}{c} \) | 翼厚比 [−] |
(出典:Fluid-Dynamic Drag, P.6-5 (2)式)
第一項は摩擦抵抗の項で、平板の摩擦抵抗係数 \( C_f \) に翼厚比 \( \displaystyle \frac{t}{c} \) を考慮した式になっています。翼型の摩擦抵抗は翼の上面・下面の2倍あるので、 \( C_f \) の前に「2」が掛けられています。
第二項は圧力抵抗の項で、こちらも翼厚比の関数になっています。
Fluid-Dynamic Dragに記載されている実験式の比較グラフに使用しているレイノルズ数を適用範囲(Re = 1~5×104)としています。
検証結果
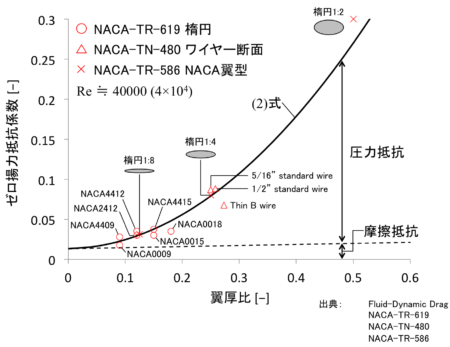
(2)式について風洞試験結果と比較を行ったのが上のグラフです。検証用データとして、NACA翼型や楕円、ワイヤー断面のゼロ揚力抵抗(風洞試験結果)を掲載しています。
遷移〜乱流領域(Re = 6×105 ~ 8×106)
\( \displaystyle C_{d_0} = 2C_f \left ( \underset{\text{摩擦抵抗}} { \underline{ 1 + 2\frac{t}{c} }} + \underset{\text{圧力抵抗}} { \underline{ 60 \left ( \frac{t}{c} \right ) ^4 }} \right ) \tag{3} \)
| \(C_{d_0}\) | ゼロ揚力抵抗係数 [−] |
| \(C_f\) | 平板の摩擦抵抗係数 [−] |
| \( \displaystyle \frac{t}{c} \) | 翼厚比 [−] |
(出典:Fluid-Dynamic Drag, P.6-6 (6)式)
こちらも第一項は摩擦抵抗、第二項が圧力抵抗を表しています。(係数は少し違いますがDATCOMに記載されている計算式と同じ形をしています。)
Fluid-Dynamic Dragによると、平板の摩擦抵抗係数 \(C_f\) の計算は遷移位置を考慮する必要があるとしています。
すなわちコード長の30%位置が遷移点だとすると、使用する平板の摩擦抵抗のうち30%は層流の摩擦抵抗、70%を乱流の摩擦抵抗とすればよいです。
\( \displaystyle C_f = C_{f_{lami}} \times t.p. + C_{f_{turb}} \times \left ( 1 – t.p. \right ) \tag{4} \)
| \(C_f\) | 平板の摩擦抵抗係数 [−] |
| \(C_{f_{lami}}\) | 平板の層流での摩擦抵抗係数 [−] |
| \(C_{f_{turb}}\) | 平板の乱流での摩擦抵抗係数 [−] |
| \(t.p.\) | 翼型における遷移位置 [−] (コード長30%位置なら0.3) |
NACA4桁シリーズの翼型では最大翼厚位置がコード長の30%位置ですので、負の圧力勾配が最大翼厚位置まであると考えられます。そのため遷移点もその付近にあると仮定して計算します。
Fluid-Dynamic Dragに記載されている実験式の比較グラフに使用しているレイノルズ数を適用範囲(Re = 6×105 ~ 8×106)としています。
検証結果
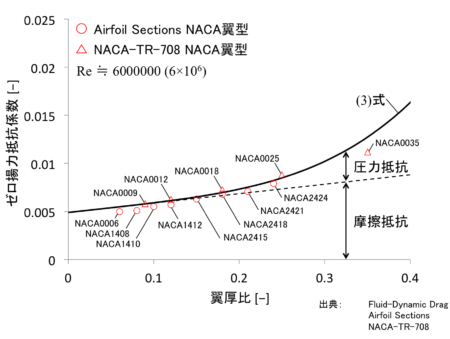
(3)式について風洞試験結果と比較を行ったのが上のグラフです。
検証用データとして、NACA4桁シリーズの翼型のゼロ揚力抵抗(風洞試験結果)を掲載しました。NACA4桁シリーズの翼型データなので遷移点をコード長の30%位置として計算しています。
翼型の揚力抵抗の推算
文献調査中。
まとめ
- 翼型のゼロ揚力抵抗は、平板の摩擦抵抗係数を使用し翼厚比をパラメータとして計算できる。
- 翼型のゼロ揚力抵抗には、翼厚による流れの加速と後縁の剥離を考慮する。
参考資料
- Fluid-Dynamic Drag, Hoerner, 1965
- Aerofoil Sections, Friedrich Wilhelm Riegels (PDFが開きます)
- NACA-TN-480: The Drag of Streamline Wires
- NACA-TR-586: Airfoil Section Characteristics as Affected by Variations of the Reynolds Number
- NACA-TR-619: Drag of cylinders of simple shapes
- NACA-TR-708: Tests of the NACA 0025 and 0035 Airfoils in the Full-Scale Wind Tunnel



コメントを残す