翼型の揚力・抵抗・ピッチングモーメントの定義式
翼型の揚力・抵抗・ピッチングモーメントは、単位翼幅あたりの力・モーメントとして以下の式で定義されます。
翼型の揚力・抵抗・ピッチングモーメント
\( \displaystyle l=\frac{1}{2}\rho {V_\infty}^2 c×C_l \tag{1}\)
\( \displaystyle d=\frac{1}{2}\rho {V_\infty}^2 c×C_d \tag{2}\)
\( \displaystyle m=\frac{1}{2}\rho {V_\infty}^2 c^2×C_m \tag{3}\)
翼型の空力係数(揚力係数・抵抗係数・ピッチングモーメント係数)
\( \displaystyle C_l = \frac{ l }{ \displaystyle \frac{1}{2} \rho {V_\infty}^2 c } \tag{4}\)
\( \displaystyle C_d = \frac{ d }{ \displaystyle \frac{1}{2} \rho {V_\infty}^2 c } \tag{5}\)
\( \displaystyle C_m = \frac{ m }{ \displaystyle \frac{1}{2} \rho {V_\infty}^2 c^2 } \tag{6}\)
| \(l\) | 単位翼幅あたりの揚力 [N] |
| \(d\) | 単位翼幅あたりの抵抗 [N] |
| \(m\) | 単位翼幅あたりのピッチングモーメント [Nm] |
| \(\rho\) | 空気密度 [kg/m3] (=1.225, 地上0m, 15℃) |
| \(V_\infty\) | 空気速度 [m/s] |
| \(c\) | コード長 [m] |
| \(C_l\) | 翼型の揚力係数 [−] |
| \(C_d\) | 翼型の抵抗係数 [−] |
| \(C_m\) | 翼型のピッチングモーメント係数 [−] |
翼型の揚力・抵抗・ピッチングモーメントとは?
空力係数とは?
翼型の揚力・抵抗・ピッチングモーメントの定義位置
翼型のピッチングモーメント(係数)は、空気合力(揚力・抵抗)の定義位置により変化します。
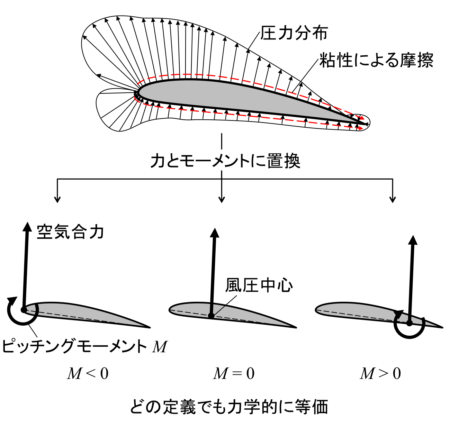
風圧中心以外に空気合力を定義する場合、差分となるピッチングモーメントを追加することで力学的に等価になります。
翼型の空気力の一般的な定義方法は以下の3つです。
- 風圧中心基準
- 空力中心基準
- 25%コード長基準
① 風圧中心基準
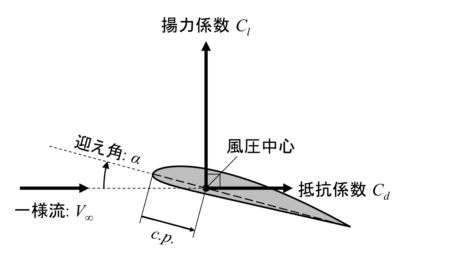
空気力の作用点である風圧中心に揚力と抵抗を定義する方法です。
実際の空気力の作用点をそのまま使用するので直感的に分かりやすい定義ですが、風圧中心は迎え角の変化とともに移動するため、扱いにくいデメリットがあります。
\(\displaystyle C_{m_0}= -c.p. \times C_n \tag{5}\)
| \(C_{m_0}\) | 前縁まわりのピッチングモーメント係数 [−] |
| \(c.p.\) | 圧力中心位置 [−] |
| \(C_n\) | 法線分力係数 [−] |
② 空力中心基準
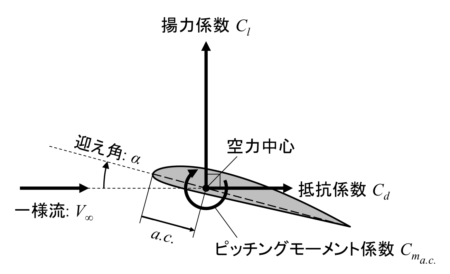
空力中心に揚力・抵抗・ピッチングモーメントを定義する方法です。
揚力と抵抗に加えて、差分となる空力中心まわりのピッチングモーメント係数 \( C_{m_{a.c.}} \) が追加されています。
空力中心に空気力を定義すると、ピッチングモーメントが一定になる利点があります。
\(\displaystyle C_{m_0}= -a.c. \times C_n + C_{m_{a.c.}} \tag{6}\)
| \(C_{m_0}\) | 前縁まわりのピッチングモーメント係数 [−] |
| \(a.c.\) | 空力中心位置 [−] |
| \(C_n\) | 法線分力係数 [−] |
| \(C_{m_{a.c.}}\) | 空力中心周りのピッチングモーメント係数 [−] |
③ 25%コード長基準
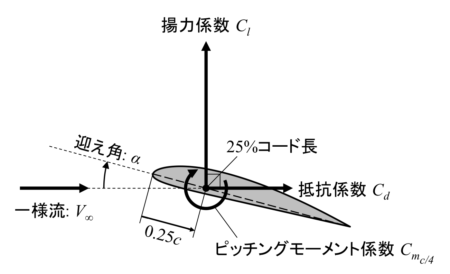
コード長の25%位置に揚力・抵抗・ピッチングモーメントを定義する方法です。
揚力と抵抗に加えて、差分となる25%コード長まわりのピッチングモーメント係数 \( C_{m_{c/4}} \) が追加されています。
風洞試験データはコード長の25%位置で整理されていることが多いです。25%コード長は理論的な空力中心ですが、翼型によって数%ずれることがあるので注意が必要です。
\(\displaystyle C_{m_0}= -0.25 \times C_n + C_{m_{c/4}} \tag{4} \)
| \(C_{m_0}\) | 前縁まわりのピッチングモーメント係数 [−] |
| \(C_n\) | 法線分力係数 [−] |
| \(C_{m_{c/4}}\) | ピッチングモーメント係数 [−] (25%コード長基準) |
コード線(翼弦線)に垂直・平行な空気力の定義式
翼型の揚力と抵抗の関係から、コード線に垂直・平行な力も幾何学的に計算できます。
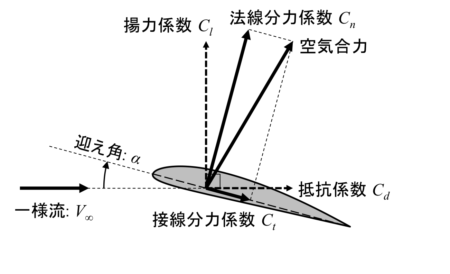
空気合力のうちコード線に対して垂直な力を法線分力(normal force)、平行な力を接線分力(tangential force)といいます。
\( C_n = C_l \cos \left ( \alpha \right ) + C_d \sin \left (\alpha \right ) \tag{7}\)
\( C_t = – C_l \sin \left (\alpha \right ) + C_d \cos \left (\alpha \right ) \tag{8}\)
\( C_l = C_n \cos \left ( \alpha \right ) – C_t \sin \left (\alpha \right ) \tag{9}\)
\( C_d = C_n \sin \left (\alpha \right ) + C_t \cos \left (\alpha \right ) \tag{10}\)
| \(C_n\) | 法線分力係数 [−] |
| \(C_t\) | 接線分力係数 [−] |
| \(C_l\) | 揚力係数 [−] |
| \(C_d\) | 抵抗係数 [−] |
| \(\alpha\) | 迎え角 [deg] |
まとめ:翼型の揚力・抵抗・ピッチングモーメントの定義
- 翼型の揚力・抵抗・ピッチングモーメントの定義方法には「風圧中心基準」「空力中心基準」「25%コード長基準」の3つある。
- コード線に垂直・平行な力は、揚力・抵抗・迎え角を用いて幾何学的に計算できる。
参考資料
次の記事
次の記事では、空力中心と風圧中心について解説します。




コメントを残す